L'énergie, conversions et transferts

I - Energie électrique⚓︎

1) Rappels⚓︎

Lois des mailles, loi des noeuds

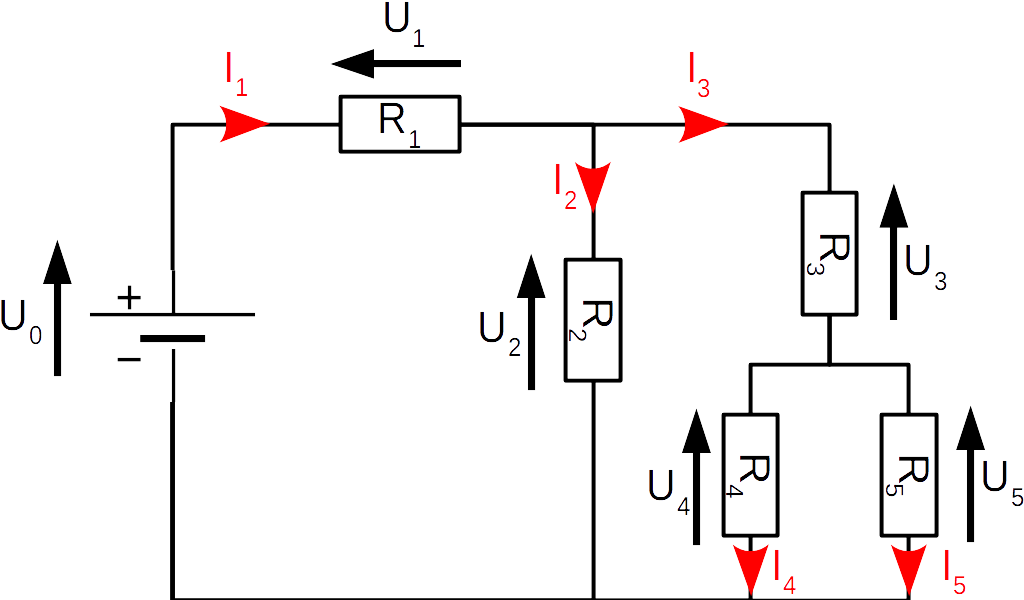
	I	U	R
0		U₀ = 5V
1	I₁ = 200mA	U₁ = 2V	R₁
2	I₂ = 50mA	U₂	R₂
3	I₃	U₃ = 1V	R₃
4	I₄ = 100mA	U₄	R₄
5	I₅	U₅	R₅

Dans le circuit ci-dessus, retrouver les valeurs manquantes.

Corrigé

On va utiliser dans ce circuit les 3 lois de l'électricité vues en 2^nde :

la loi des noeuds : La somme des intensités entrantes dans un noeud est égale à la somme des intensités sortantes
la loi des mailles : Dans une maille donnée la somme des tensions aux bornes des dipôles qui la composent est nulle
la loi d'Ohm : Aux bornes d'un conducteur ohmique, U = R × I

Les intensités :

Le premier noeud nous donne I₁ = I₂ + I₃
I₃ = I₁ - I₂ = 200 - 50 = 150mA
Le premier noeud nous donne I₃ = I₄ + I₅
I₅ = I₃ - I₄ = 150 - 100 = 50mA

Les tensions :

La première maille nous donne U₀ = U₁ + U₂
U₂ = U₀ - U₁ = 5 - 2 = 3V
La seconde maille donne U₂ = U₃ + U₄
U₄ = U₂ - U₃ = 3 - 1 = 2V
Enfin, la dernière petite maille nous indique que U₅ = U₄ = 2V

Les résistances :

R₁ = U₁/I₁ = 2 / 0.2 = 10Ω
R₂ = U₂/I₂ = 3 / 0.05 = 60Ω
R₃ = U₃/I₃ = 1 / 0.05 = 20Ω
R₄ = U₄/I₄ = 2 / 0.1 = 20Ω
R₅ = U₅/I₅ = 2 / 0.05 = 40Ω

2) Puissance⚓︎

Définition

La puissance est la vitesse à laquelle est transférée/convertie une énergie.

Elle s'exprime en watts et 1W = 1J.s^-1.

On peut également écrire cette relation : ΔE = P×Δt
avec ΔE (J), P (W) et Δt (s)

L'énergie électrique fournie à un appareil électrique parcouru par un courant d'intensité I et aux bornes duquel est appliquée une tension U vaut :

P = U×I

Avec P (W), U (V) et I (A).

Application

Cette bouilloire disponible sur un site de vente en ligne est annoncée comme ayant une puissance de 2200W.

Quelle intensité parcourt la résistance électrique lors de son fonctionnement nominal ?
Quelle est la valeur de la résistance chauffante présente dans cette bouilloire ?

Corrigé

On utilise la relation P = U×I avec U=230V (tension du secteur).
$I = \frac{P}{U} = \frac{2200 W}{230 V} = 9, 57 A$
On utilise la loi d'Ohm U = R×I
$R = \frac{U}{I} = \frac{230 V}{9, 57 A} = 24 Ω$

3) Energie électrique⚓︎

Relation

En combinant les 2 formules présentées au paragraphe précédent,P = U×I et ΔE = P×ΔT, on trouve que :

ΔE = U×I×Δt

Avec ΔE (J), U (V), I (A) et ΔT (s).

Application

On verse dans la bouilloire précédente 1,3L d'eau à 17°C. Combien de temps faudra-t-il attendre pour que l'eau soit à température idéale pour un thé, soit environ 80°C ?
(il paraît qu'il ne faut pas faire bouillir l'eau dans laquelle le thé va infuser sous peine de perdre en arômes)

Corrigé

On va d'abord calculer l'énergie nécessaire pour faire passer 1,3L d'eau de 17°C à 80°C :

$Δ Q_{e a u} = V_{e a u} \times ρ_{e a u} \times c_{e a u} \times (T_{f} - T_{i})$

donc :

$Δ Q_{e a u} = 1, 3 L \times 1000 g . L^{- 1} \times 4.18 J . ° C^{- 1} . g^{- 1} \times (80 - 17) = 3, 42 \times 10^{5} J$

On calcule maintenant le temps nécessaire à la résistance pour transférer cette chaleur par effet Joule :

$Δ E = P \times Δ t \Rightarrow Δ t = \frac{Δ E}{P} \Rightarrow Δ t = \frac{3, 42 \times 10^{5} J}{2200 W} = 155 s$

L'eau sera donc à température idéale en 2min 35s.

Remarque

Il est possible de combiner la loi d'Ohm et l'expression de la puissance dans un appareil électrique : cela permet de calculer les pertes par effet joule. En effet, $U = R \times I$ et $P = U \times I$ donnent :

$P = R \times I^{2} = \frac{U^{2}}{R}$

II - Energie mécanique⚓︎

1) Energie cinétique⚓︎

Définition

L'énergie cinétique est l'énergie nécessaire pour accélérer un objet de masse m immobile jusqu'à une vitesse v.

$E_{c} = \frac{1}{2} \times m \times v^{2}$

Avec :

E_c : Energie cinétique en J,
m : Masse en kg,
v : vitesse en m.s^-1

Remarque

Cette formule n'est valable que si la vitesse de l'objet est petite devant la vitesse de la lumière dans le vide (sinon la formule est plus compliquée).

Application

Quicksilver est un personnage de l'Univers Marvel capable de se déplacer très vite. Quelle est son énergie cinétique lorsqu'il se déplace à 5 fois la vitesse du son, soit Mach 5 ?

Corrigé

Le son au niveau du sol se propage à environ 340m.s^-1, ce qui fait que Quicksilver se déplace à une vitesse de 340×5 = 1700m.s^-1.

Si on fait l'hypothèse qu'il a une masse de 70kg, il est possible d'appliquer la formule :
$E_{c} = \frac{1}{2} \times m \times v^{2}$

Application numérique :
$E_{c} = \frac{1}{2} \times 70 \times 1700^{2} = 1.01 \times 10^{8} J$

Il apparaît donc que Quicksilver doit être un gros mangeur puisque cette énergie correspond à environ 8 fois l'apport énergétique nutritionnel quotidien recommandé !

2) Travail d'une force⚓︎

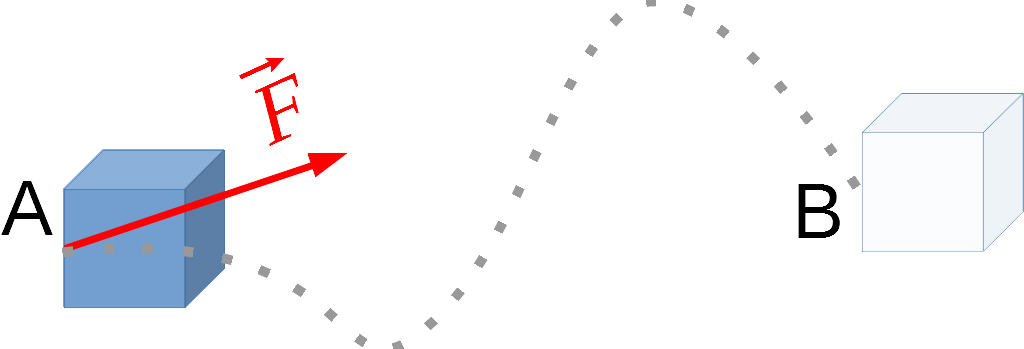
A savoir

Si une force $\vec{F}$ s'applique sur un objet tout au long d'un trajet allant de A à B, alors le travail de cette force vaut :
$W = \vec{F} \cdot \vec{A B} = ‖ \vec{F} ‖ \times ‖ \vec{A B} ‖ \times c o s (\vec{F}, \vec{A B})$

Théorème de l'énergie cinétique

Entre 2 positions successives d'un objet, la variation ΔE_C d'énergie cinétique est égale au travail des forces s'exerçant sur cet objet entre ces 2 positions :

$Δ E_{C} = \sum_{} \vec{F} \cdot \vec{A B}$

Application

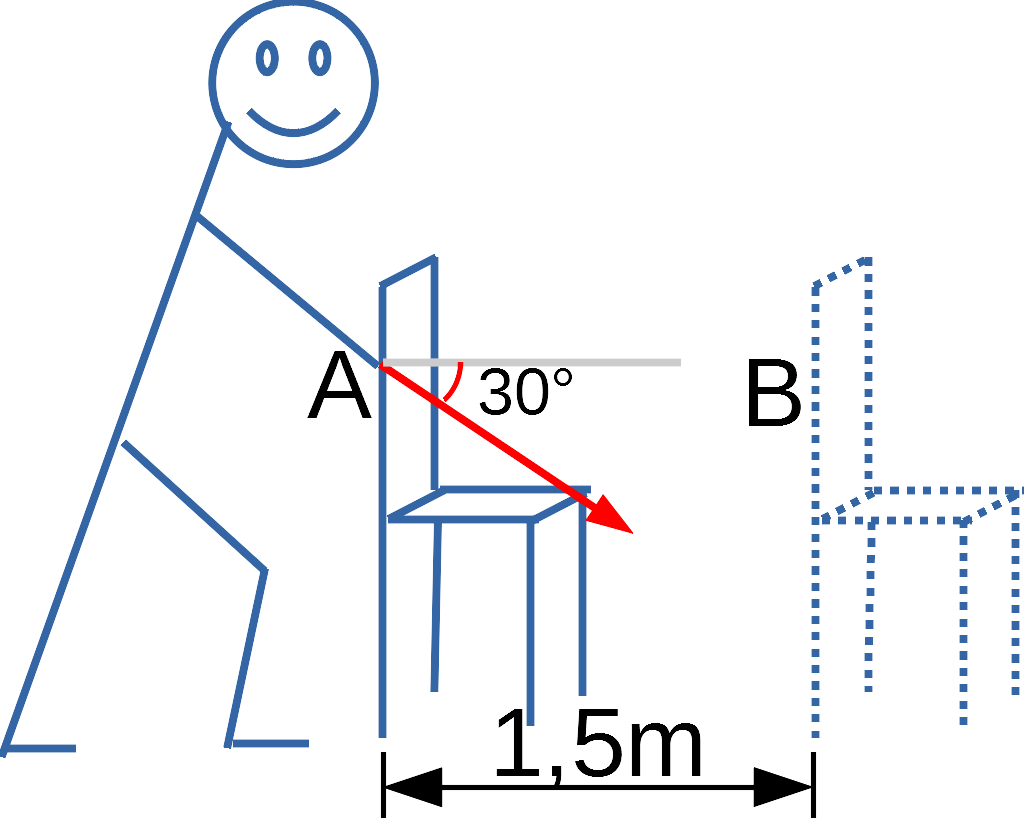
Pierre pousse une chaise sur une distance AB=1,5m selon le schéma ci-dessus. Il exerce de façon continue une force de 100N.

Corrigé

Le travail de la force vaut :

$W = \vec{‖ F ‖} \times ‖ \vec{AB} ‖ \times c o s (\vec{F}, \vec{AB}) = 1, 5 \times \cos (30) = 130 N$

3) Energie de position⚓︎

Définition

L'énergie de position est l'énergie nécessaire pour soulever un objet de masse m d'un point A à un point B :

$E_{p} = m \times g \times Δ h$

Avec :

E_p : Energie de position en J,
m : Masse en kg,
g : intensité de pesanteur en N.kg^-1
Δh : variation d'altitude en m.

Remarque

Cette formule n'est valable que si l'on fait l'hypothèse d'un champ de gravitation uniforme (sinon la formule est plus compliquée).

Application

Arnold soulève une haltère de 110kg en développé-couché. Quelle énergie fournit-il à l'haltère lorsqu'il la fait passer de son buste jusqu'à bout de bras ?

Corrigé

Si on fait l'hypothèse qu'Arnold soulève l'haltère de 60cm, il est possible d'appliquer la formule :
$E_{p} = m \times g \times Δ h$

Application numérique :
$E_{p} = 110 \times 9, 81 \times 0, 6 = 647, 5 J$

4) Energie mécanique⚓︎

Definition

L'énergie mécanique d'un objet représente la somme de son énergie de position et de son énergie cinétique.

$E_{m} = E_{c} + E_{p}$

Conservation de l'énergie mécanique⚓︎

Lorsque l'on jette un objet verticalement vers le haut, celui-ci quitte notre main avec une vitesse initiale donnée, qui diminue rapidement, s'annule au moment où l'objet atteint sont altitude maximale et réaugmente mais dans le sens inverse lorsqu'il retombe.
Cela signifie que son énergie cinétique varie au cours de sa trajectoire. Comme écrit dans l'introduction de ce chapitre, l'énergie ne disparaît pas, elle se transforme.

On en déduit donc que l'énergie cinétique de l'objet se transforme en un autre type d'énergie. Si l'on néglige les frottements de l'air, alors elle ne peut se convertir qu'en énergie de position.

L'objet quitte notre main avec une énergie Ec donnée, qui se transforme peu à peu en énergie de position Ep. Arrivé à sa hauteur maximale, toute l'énergie cinétique selon l'axe vertical s'est transformée en énergie de position. Lorsqu'il retombera, cette énergie de position se convertira de nouveau en énergie cinétique.

Conservation de l'énergie mécanique

Lorsqu'un objet est lancé librement et sans frottement, entre 2 positions arbitraires A et B de sa trajectoire, on peut écrire :

$E_{c_{A}} + E_{p_{A}} = E_{c_{B}} + E_{p_{B}}$

Application

Kermit est une petite grenouille de masse m=50g. Pour attraper Droso la mouche qui vole au-dessus d'elle, elle effectue un bond de 80cm de hauteur.

Quelle était sa vitesse initiale en début de saut ?

Corrigé

On va utiliser la conservation de l'énergie mécanique pour répondre à cette question : A est le point de départ de la grenouille où on cherche sa vitesse initiale et B, le point d'altitude maximale où elle attrape la pauvre Droso.

On considère qu'au point A l'altitude est nulle (il nous sert d'origine) et qu'au point B c'est sa vitesse qui est nulle puisqu'elle a atteint son altitude maximale.

On a donc $E_{c_{A}} + E_{p_{A}} = E_{c_{B}} + E_{p_{B}}$ avec $E_{p_{A}} = 0$ et $E_{c_{B}} = 0$ .

Donc : $E_{c_{A}} = E_{p_{B}}$

Application numérique:
$\frac{1}{2} \times m \times {v_{A}}^{2} = m \times g \times h_{B}$

soit : $v_{A} = \sqrt{2 \times g \times h_{B}} = \sqrt{2 \times 9, 81 \times 0, 8} = 3, 96 m . s^{- 1}$

III - Conversion d'énergie au cours d'une combustion⚓︎

Mesurer une énergie de combustion⚓︎

On peut mesurer l'énergie dégagée par la combustion d'un gaz comme le butane en mesurant de combien s'est réchauffée une quantité d'eau déterminée, comme le montre l'expérience ci-dessous :

Energie de liaison⚓︎

Voir la vidéo du cours