Mouvement et interactions

I- Pression

1) Force pressante

Modélisation de la force pressante due à l'air contenue dans le ballon

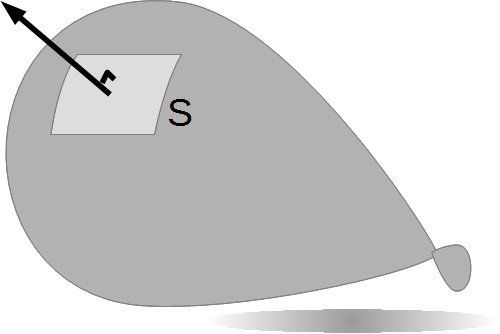
Lorsque notre doigt appuie sur le piston d'une seringue ou quand on marche sur la neige avec des raquettes ou des skis, on crée une force pressante sur le milieu opposé (gaz pour la seringue, neige pour les skis).

Cette force est notée $\overrightarrow{F}$.

Ses caractéristiques, comme toutes les forces, sont son point d'application, sa direction, son sens et son intensité. Cependant dans le cas d'une force pressante, cela dépend de la surface sur laquelle elle s'applique :

• le point d'application est au centre de la surface étudiée
• la direction est perpendiculaire à la surface
• le sens est du milieu applicateur vers le milieu pressé

2) Définition d'une pression

La notion de pression s'applique à tous les fluides (substance n'ayant pas de forme propre, comme les gaz ou les liquides).

Pression

Si un fluide exerce une action mécanique modélisée par une force pressante d'intensité F sur une surface d'aire S, alors on appelle pression P du fluide sur la surface la grandeur donnée par :

$P=\frac{F}{S}$

F s'exprime en newton (N) S s'exprime en metre carré (m2) P s'exprime en pascal (Pa)

L'unité S.I. pour exprimer la pression est donc le pascal (Pa), qui vaut (unité SI oblige) 1 Pa = 1 N.m^-2

Dans la pratique, 1 Pa est une valeur de pression minuscule comparée à celle de l'atmosphère (101 300 Pa par beau temps), on a donc plutôt l'habitude d'utiliser des hectopascals (hPa).

De plus d'autres unités sont également utilisées :

• le bar : 1 bar = 10⁵ Pa
• l'atmosphère : 1 atm = 1.013 x 10⁵ Pa
• le millimètre de mercure : 760 mmHg = 1 atm

Cette dernière unité vous semble bizarre ? Elle est pourtant très utilisée en médecine !
Quand le médecin prend votre tension et vous dit "C'est bon, vous avez 12 - 8" Il parle en fait de votre pression qui vaut 120 mmHg et 80 mmHg (systolique / diastolique)

3) Relation entre pression et volume

Lorsque l'on bouche l'extrêmité d'une seringue avec notre doigt et que l'on essaie de comprimer le gaz piégé en appuyant sur le piston, On sent bien qu'il est de plus en plus difficile d'appuyer au fur et à mesure que l'on diminue l'espace disponible.

Il est donc évident qu'il existe une relation entre le volume et la pression d'une quantité de gaz donné.

Déterminer cette relation est le but de la première partie du TP n°09.

Il est possible de faire cette expérience "en ligne" à l'aide d'une animation réalisée par Jean-Pierre Fournat et disponible sur son site internet : cliquez ici !

Démarche : relevez dans un tableur (LibreOffice Calc) la valeur de la pression tout en faisant varier le volume de la seringue de 10mL en 10mL. Vous devriez obtenir ce tableau :

Volume (mL)	Pression (hPa)	Pression-1 (hPa-1)
20	2500	4,00x10-4
30	1700	5,88x10-4
40	1300	7,69x10-4
50	1000	1,00x10-3
60	850	1,18x10-3
70	750	1,33x10-3
80	650	1,54x10-3
90	550	1,82x10-3
100	500	2,00x10-3

Il suffit ensuite de tracer deux graphiques avec le volume en abscisses, l'un avec la pression en ordonnées et l'autre avec son inverse :

On voit sur ce graphique la relation que l'on envisageait : plus le volume est faible et plus la pression est grande.

Sur ce graphique en revanche, la relation de proportionnalité entre V et 1/P est évidente : les points de mesure sont alignés sur une droite qui passe par l'origine.
Cela démontre la loi de Boyle-Mariotte qui dit que pour une quantité de gaz donnée on a : $$P\times V=\mathrm{constante}$$

4) Relation entre pression et profondeur

a) La pression hydrostatique

(Youtube) Une vidéo de l'apnéiste Français Guillaume Néry capable de plonger à -125m

Tout corps plongé dans un fluide (liquide ou gaz) subit une pression due au poids du fluide situé au-dessus de lui.

Ainsi, plus un plongeur s'enfonce, plus la pression hydrostatique qu'il subit est importante.

Le but de la deuxième partie du TP n°25 était de déterminer la relation entre la profondeur et la pression hydrostatique.

On a déterminé qu'elle augmentait d'un bar tout les 10 mètres.

b) Pression absolue et pression relative

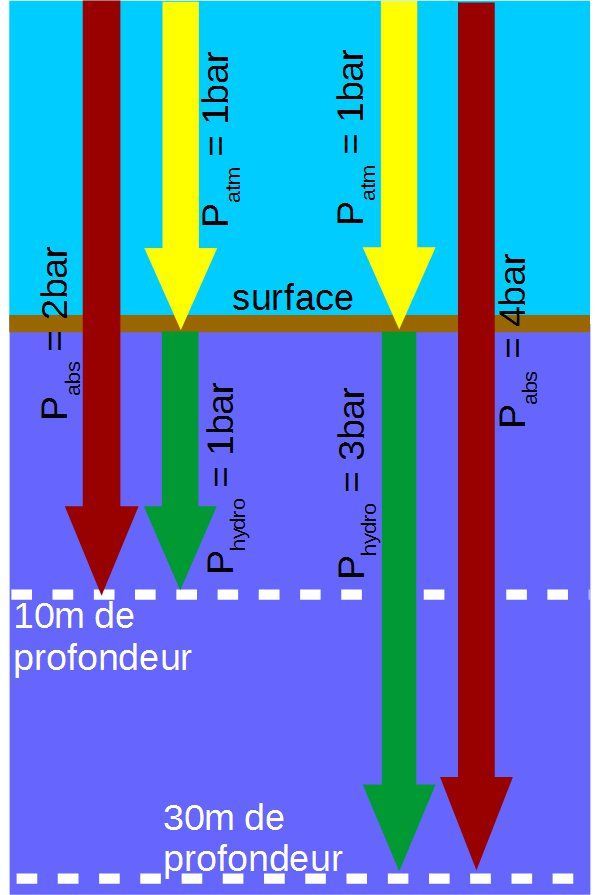
En plus de la pression due à l'eau le plongeur est soumis à la pression atmosphérique comme toute personne présente hors de l'eau. Lorsqu'il plonge, la pression hydrostatique va peu à peu s'ajouter à la pression atmosphérique.

On appelle pression absolue P_abs la pression totale subie par le plongeur. Elle est la somme de la pression atmosphérique P_atm et de la pression hydrostatique P_hydro qu'il subit.

$$P_{\mathrm{abs}}=P_{\mathrm{atm}}+P_{\mathrm{hydro}}$$

c) Mesurer une pression

La pression se mesure à l'aide d'un manomètre. Certains mesurent la pression relative (comme le manomètre qui sert à mesurer la pression des pneus) d'autres permettent de mesurer la pression absolue (celui utilisé en TP) et sont aussi appelés pressiomètres.

Un baromètre mesure la pression atmosphérique.

d) Solubilité d'un gaz dans un liquide

(Youtube) Que se passe-t-il l'orsque l'on ouvre une bouteille d'eau gazeuse à 3850m d'altitude ?

C'est une expérience de la vie quotidienne : vous ouvrez pour la première fois une bouteille d'eau gazeuse ou de soda. Des bulles apparaissent dans la bouteille en même temps que le "pschiiit" d'un dégagement gazeux.

Le gaz n'est pas apparu subitement, il était dissout dans l'eau et restait dissout tant que la pression à l'intérieur de la bouteille était suffisante.
En ouvrant la bouteille, vous avez fait chuter brusquement la pression, qui est devenue insuffisante pour laisser le gaz dissout dans l'eau. Celui-ci s'est donc échappé.

De même, un plongeur en bouteille respire en profondeur un gaz à la même pression que celle qui l'entoure. Ce faisant, son sang dissout une plus grande quantité de gaz que s'il se trouvait à la surface.

Lors de sa remontée, la capacité de son sang à dissoudre le gaz va diminuer et si le plongeur va trop vite des bulles de gaz vont se former dans son corps : c'est l'accident barotraumatique.

C'est la raison pour laquelle au-delà d'une certaine profondeur, il est nécessaire de respecter des périodes d'arrêt appelées paliers de décompression pour permettre au gaz excédentaire de s'évacuer par les poumons.

II- Les forces gravitationnelles et électromagnétiques

1) L'interaction gravitationnelle

Deux corps de masses m₁ et m₂ dont les centres de gravité respectifs sont distants d'une distance d s'attirent avec une force mutuelle F_g dont l'expression est :

Interaction gravitationnelle

$F_g=G\times \frac{m_1\times m_2}{d^2}$

• F_g, force d'attraction gravitationnelle en newtons (N)
• m₁, m₂ en kilogrames (kg)
• d, distance en mètres (m)
• G, constante de gravitation universelle
• G = 6.67×10^-11N.m².kg^-2

2) L'interaction électrostatique

Deux corps de charges q₁ et q₂ séparés par une distance d exercent avec une force mutuelle F_em dont l'expression est :

Interaction électrostatique

$F_{em}=k\times \frac{\left|q_1\right|\times \left|q_2\right|}{d^2}$

• F_em, force électromagnétique en newtons (N)
• q₁, q₂ charge électrique en coulombs (C)
• d, distance en mètres (m)
• k, constante de Coulomb
• k = 9,0×10⁹N.m².C^-2 dans le vide.

3) Applications

Calculer une force d'attraction

Rayan Montaigu et Jamie-Lee Capulet ayant épuisé leurs forfaits téléphoniques respectifs, sont obligés de se parler au balcon.

Calculer leur attraction gravitationnelle réciproque sachant que Rayan a une masse de 70kg, qu'ils sont séparés d'une distance de 3m et qu'on ne demande pas son poids à une fille, mais que ce ne doit pas être loin de 60kg.

Réponse

$F_{Rayan/Jamie-Lee}=G\times \frac{m_1\times m_2}{d^2}$
$F_{Rayan/Jamie-Lee}=6,67\times {10}^{-11}\times \frac{70\times 60}{3^2}$
$F_{Rayan/Jamie-Lee}=3,11\times {10}^{-8}N$

Trouver une masse

Issam a une masse de 65kg et un poids de 637.7 N à la surface de la Terre.
Calculer la masse de notre planète sachant que son rayon est de 6370km

Réponse

$F_{Terre/Issam}=G\times \frac{m_{Terre}\times m_{Issam}}{{R_T}^2}$

/! Attention à convertir le rayon en mètres !

$m_{Terre}=\frac{F_{Terre/Issam}\times {R_T}^2}{G\times m_{Issam}}$

$m_{Terre}=\frac{637.7\times {\left(6,37\times {10}^6\right)}^2}{6,67\times {10}^{-11}\times 65}$

$m_{Terre}=5,97\times {10}^{24}\mathrm{kg}$

Gravitation VS électrostatique

1- Calculer la force d'attraction gravitationnelle avec laquelle un électron est attiré par un proton distant de 1,0×10^-10m.

• Masse électron : 9,1×10^-31kg
• Masse proton : 1,67×10^-27kg

Réponse

$F_{p/e}=G\times \frac{m_p\times m_e}{d^2}$
$F_{p/e}=6,67\times {10}^{-11}\times \frac{9,1\times {10}^{-31}\times 1,67\times {10}^{-27}}{{\left({10}^{-10}\right)}^2}$
$F_{p/e}=1,01\times {10}^{-47} N$

2- Calculer la force électrostatique entre un électron et un proton distant de 1,0×10^-10m.

• Charge électron : -1,6 × 10^-19C
• Charge proton : 1,6 × 10^-19C

Réponse

Les charges étant de signe opposé, la force est attractive $F_{p/e}=k\times \frac{\left|q_p\right|\times \left|q_e\right|}{d^2}$

$F_{p/e}=9,0\times {10}^9\times \frac{{\left(1,6\times {10}^{-19}\right)}^2}{{\left({10}^{-10}\right)}^2}$

$F_{p/e}=2,3\times {10}^{-8} N$

On remarque que du point de vue d'un électron, la force d'attraction électromagnétique d'un proton est $\frac{F_{em}}{F_g}=\frac{2,3\times {10}^{-8}}{1,01\times {10}^{-47}}=2,3\times {10}^{39}$ fois plus forte que son attraction gravitationnelle.

III - Les champs

1) Introduction

Pour pouvoir étudier les mouvements des particules, il est parfois nécessaire de connaîtres les forces qui s'exercent sur eux en fonction de l'endroit où ils se trouvent. Un champ est une cartographie d'une grandeur physique qui peut être un moyen d'y répondre.

Il est fortement recommandé de revoir le TP 8 pour se rafraîchir la mémoire.

2) Différents types de champs

Une grandeur physique peut être représentée de diverses manières et les champs peuvent donc cartographier différents types d'objets mathématiques :

Grandeurs scalaires	Grandeurs vectorielles
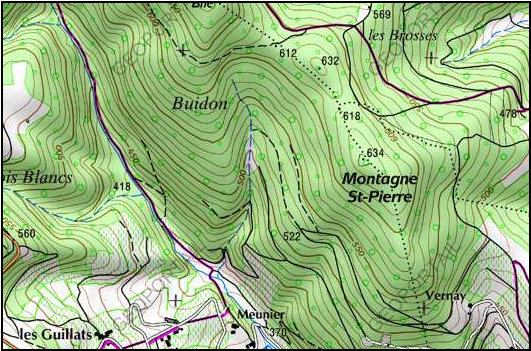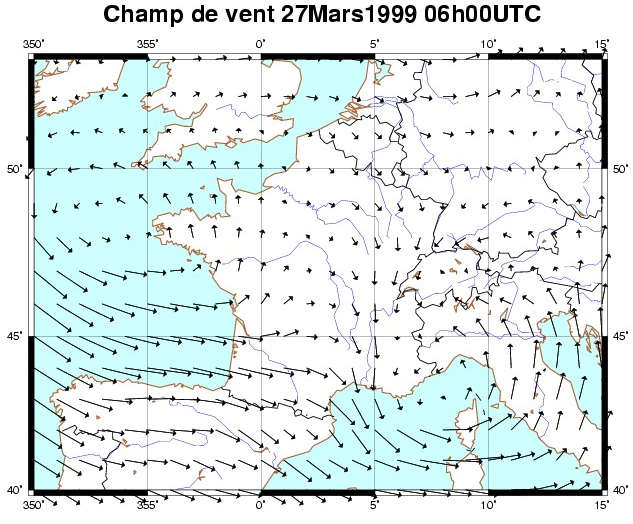Ici, la carte topographique représente un champ d'altitude	Ici la carte représente un champ vectoriel de vents

Définition

Un champ scalaire est un objet qui à chaque point de l'espace étudié associe une grandeur physique sous la forme d'un nombre réel.

Un champ vectoriel est un objet qui à chaque point de l'espace étudié associe une grandeur physique sous la forme d'un vecteur.

3) Représentation par des lignes

Champs scalaires

Les valeurs numériques ne peuvent être écrites en tout point de la carte, car celle-ci deviendrait illisible. Pour cette raison, sur les cartes topographiques, telle que la carte vue au 2), on ne représentera que certaines valeurs particulières (les sommets et les plaines par exemple) et l'on tracera des courbes de niveau reliant tous les points ayant une même altitude. Lorsque l'on étudie autre chose qu'une altitude, on peut également parler de courbes équipotentielles

Application :

En hydrologie, il est courant d'utiliser une carte topographique pour prévoir dans quelle direction une goutte de pluie va ruisseler une fois au sol : elle coulera perpendiculairement aux lignes de niveau.

Champs vectoriels

Il sera de même impossible de représenter les vecteurs associés à chque point de l'espace de façon exaustive et pour cette raison, on représentera des lignes de champs : en partant d'un point donné, on suivra l'orientation du vecteur de ce point pour rejoindre le point suivant et ainsi de suite.

Application :

Une ligne de champ sur la carte des vents donnée ci-dessus rerésenterait la trajectoire d'un grain de poussière dans l'atmosphère

Propriétés

Lignes de champs d'une aile d'avion

les lignes de champ plus ressérées montrent que la vitesse de l'air est plus importante au-dessus qu'en-dessous (c'est ce qui crée la portance de l'aile).

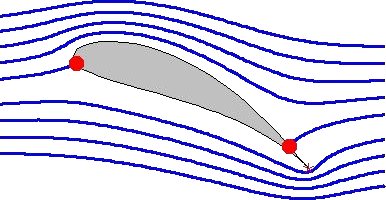
Plus des des lignes de niveau sont proches et plus la valeur varie rapidement (exemple :la pente est abrupte pour l'altitude)

Plus des des lignes de champ sont proches et plus la norme du vecteur associé à la grandeur physique est grande.

4) Le champ de gravitation

Loi de gravitation universelle

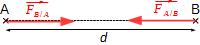
La formule de la loi de gravitation vue plus haut peut être écrite sous forme vectorielle :

$\overrightarrow{F_{A/B}}=G\times \frac{m_A\times m_B}{d^2}\overrightarrow{u}$

Où $\overrightarrow{F_{A/B}}$ est le vecteur modélisant la force que l'objet A exerce sur l'objet B.

Si l'on regarde cette formule, on se rend compte que le membre en rouge :

$\overrightarrow{F_{A/B}}=G\times \frac{m_A\times m_B}{d^2}\overrightarrow{u}$

sera le même pour tous les objets présents à priximité de l'objet A.

Cette partie $G\times \frac{m_A}{d^2}\overrightarrow{u}$ est la représentation du champ de gravitation de l'objet A.

Champ de gravitation

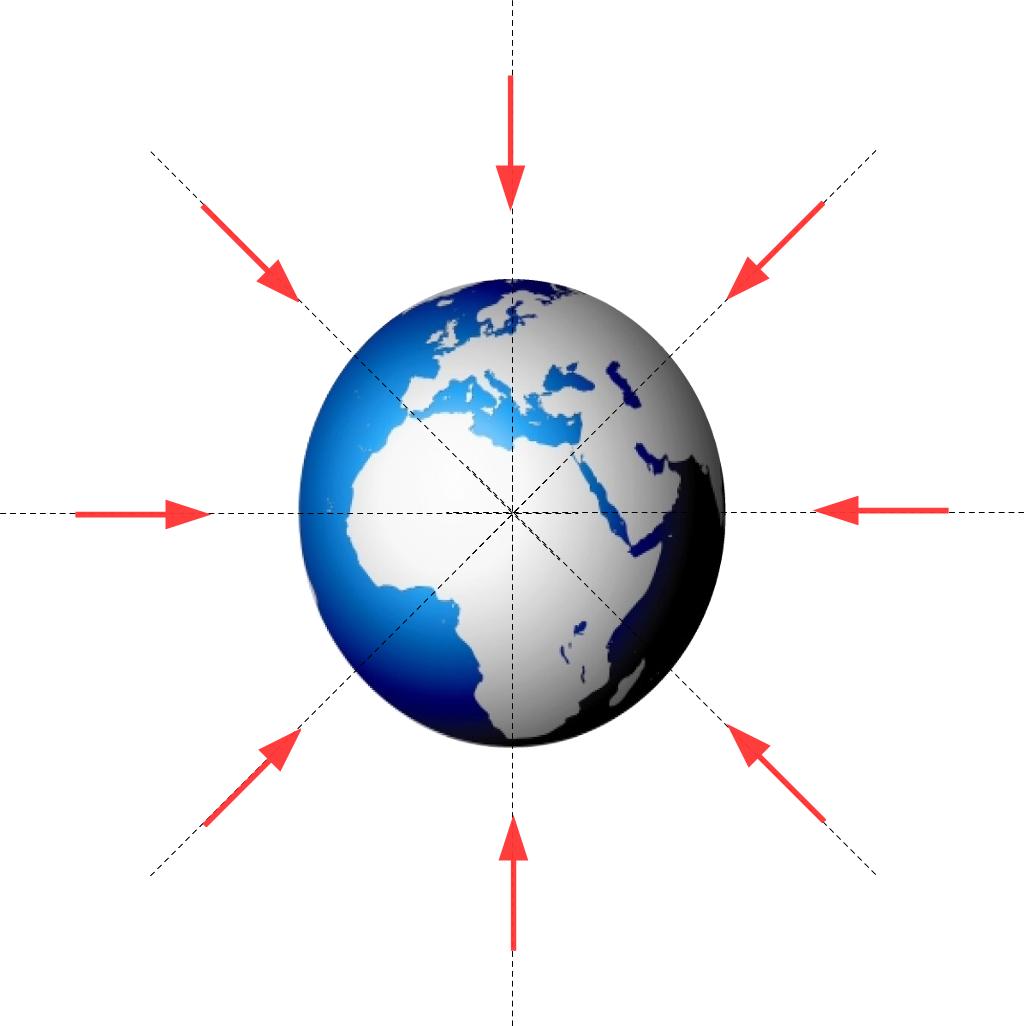
A savoir

Un champ de gravitation règne en un point de l'espace si un objet de masse m subit une action mécanique d'attraction gravitationnelle du fait de la présence d'un autre objet massif.

La force d'attraction est modélisée par une flèche ayant pour origine le centre de gravité de l'objet attiré, pour direction l'axe reliant les centres de gravités des deux objets en présence et orienté vers le centre de gravité de l'objet attracteur.

Champ de pesanteur terrestre au voisinage du sol

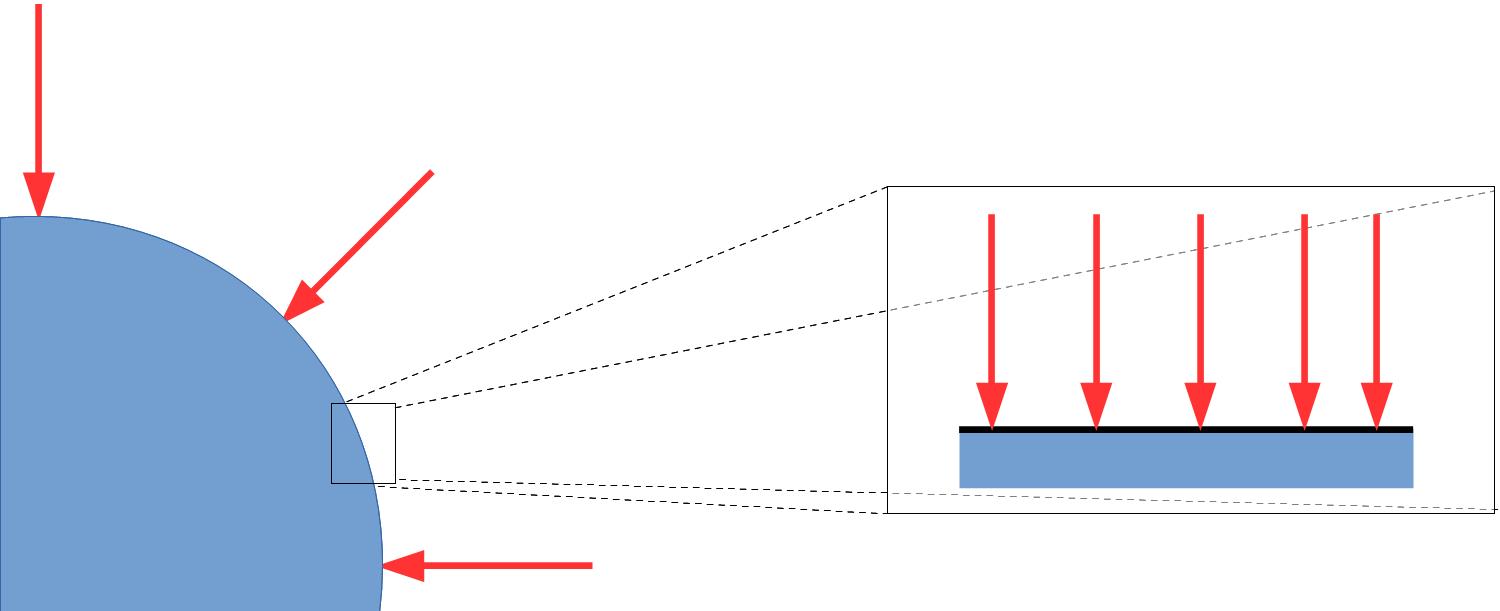
Champ uniforme

Sur Terre, au voisinage du sol, on peut considérer pour des distances petites relativement à la taille de la Terre que le champ de pesanteur est uniforme : la pesanteur est la même en tout point de la zone

Ce champ de pesanteur a pour valeur : $\vec{\zeta }=G\times \frac{m_T}{{R_T}^2}$

$\vec{\zeta }=6\mathrm{,67}\times {10}^{-11}\times \frac{5\mathrm{,97}\times {10}^{24}}{{(6\mathrm{,37}\times {10}^6)}^2}$

$\vec{\zeta }=9\mathrm{,8}N\mathrm{.}{\mathit{kg}}^{-1}=\vec{g}$

5) Le champ magnétique

A savoir

Visualisation

Lignes de champ d'un aimant. Trouvé sur Voyagesaucoeurdelascience.fr

Un champ magnétique règne en un point de l'espace si une action mécanique s'exerce sur une aiguille aimantée.

Lorsqu'une boussole est approchée d'une aimant, celle-ci s'aligne sur les lignes de champ comme la limaille de fer, son pôle sud (blanc) pointant en direction du pôle Nord de l'aimant.

Orientation

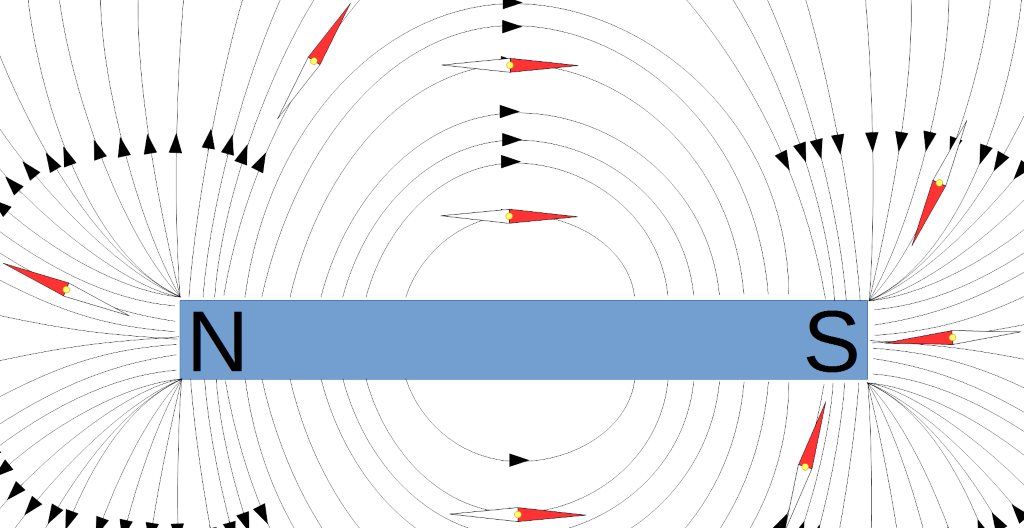
Lorsqu'une boussole est approchée d'une aimant, celle-ci s'aligne sur les lignes de champ comme la limaille de fer, son pôle sud (blanc) pointant en direction du pôle Nord de l'aimant.

6) Le champ électrostatique

Définition

Note

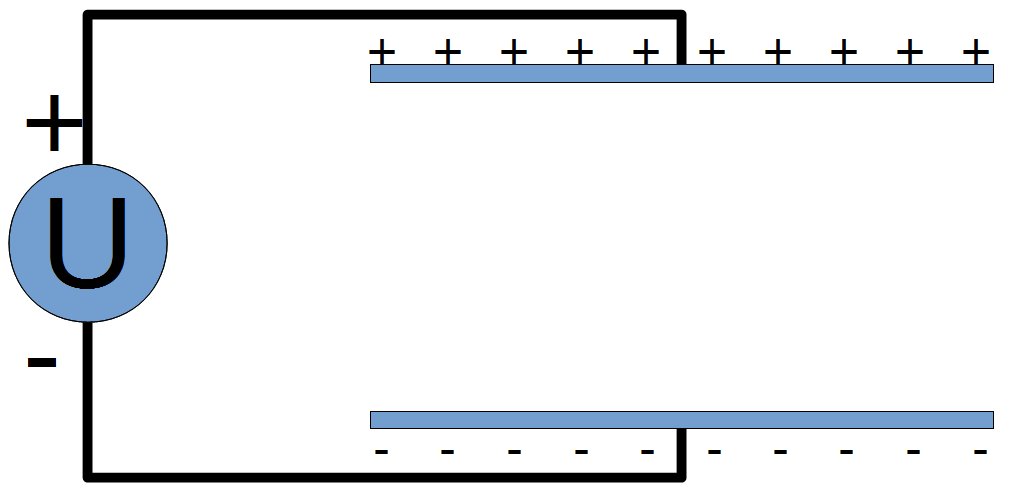
Il existe un champ électrostatique en un point de l'espace lorsqu'une particule chargée électriquement y subit une action mécanique d'origine électrostatique.

Un générateur branché à deux électrode crée un excès de charges + d'un côté (cathode) et un excès de charges - de l'autre (l'anode).

De ce déséquilibre apparaît un champ électrostatique $\overrightarrow{E}$

Une particule chargée électriquement d'une charge q subira une force $\overrightarrow{F}$

$\overrightarrow{F} = q\times \overrightarrow{E}$

IV- Mouvement et forces

1) Rappels

Ce chapitre s'appuie sur ce qui a été vu en classe de seconde sur les référentiels, la représentation des forces et le mouvement.

Cliquez ici pour vous rafraîchir la mémoire.

2) Etude d'un mouvement

a. Outils nécessaires

Les programmes demandant explicitement d'utiliser un langage de programmation pour modéliser le mouvement, Il est nécessaire d'utiliser 2 logiciels :

• Un logiciel de pointage qui permettra d'étalonner et de pointer les positions successives d'un mobile. Pymecavideo le fait très bien. lien de téléchargement, et n'a pas de limitation sur le format de vidéo.
• Un environnement de programmation comme Edupython que l'on utilise en classe, pour traiter les positions fournies par pymecavideo et tracer les graphique.

b. Le TP

Ce travail a été abordé dans le TP n°10 (cliquez ici pour le sujet).
Le script python fourni est à compléter :

Afficher le code

🐍 Script Python

import matplotlib.pyplot as plt

# coordonnées de l'objet
# pas de temps (en secondes)
delta_t=0.04 # pas de temps entre 2 positions
# Recopier ici les valeurs des positions des points obtenus dans l'atelier scientifique
x=[ ];
y=[ ];

# calcul du vecteur vitesse
if len(x) != len(y):
    print("problème de saisie, il n'y a pas le même nombre de points en x et en y !")

# Calcul du vecteur vitesse
v_x , v_y = [ ] , [ ] #on crée 2 listes vides
for i in range(1, len(x) - 1): #on va remplir les listes au fur et à mesure
    v_x.append((x[i + 1] - x[i - 1]) / (2 * delta_t))
    v_y.append((y[i + 1] - y[i - 1]) / (2 * delta_t))

# Calcul de la variation de vitesse
a_x , a_y = [ ] , [ ] # on crée 2 listes vides
for i in range(1, len(v_x) - 1): # on va remplir les listes au fur et à mesure
    a_x.append((v_x[i + 1] - v_x[i - 1]) / (2 * delta_t))
    a_y.append((v_y[i + 1] - v_y[i - 1]) / (2 * delta_t))

### Tracé des vecteurs normalisés
plt.rcParams['axes.formatter.use_locale'] = True
plt.figure(1, figsize = (5, 5))
vitesse = plt.quiver(x[1 : -1] , y[1 : -1], v_x, v_y, color = "green", width=0.003)
plt.quiverkey(vitesse, X = 0.3, Y = 1.1, U = 10, label = 'Vitesse', labelpos = 'E')
acceleration = plt.quiver(x[1 : -1], y[1 : -1], a_x, a_y, color = "red", width = 0.003)
plt.quiverkey(acceleration, X = 0.3, Y = 1.1, U = 10,label = 'acceleration', labelpos = 'E')
plt.plot(x, y, "r.")
plt.legend(loc = 'upper right')
plt.xlabel("x (m)")
plt.ylabel("y (m)")
plt.title("Trajectoire de l'objet")
plt.show()

Note

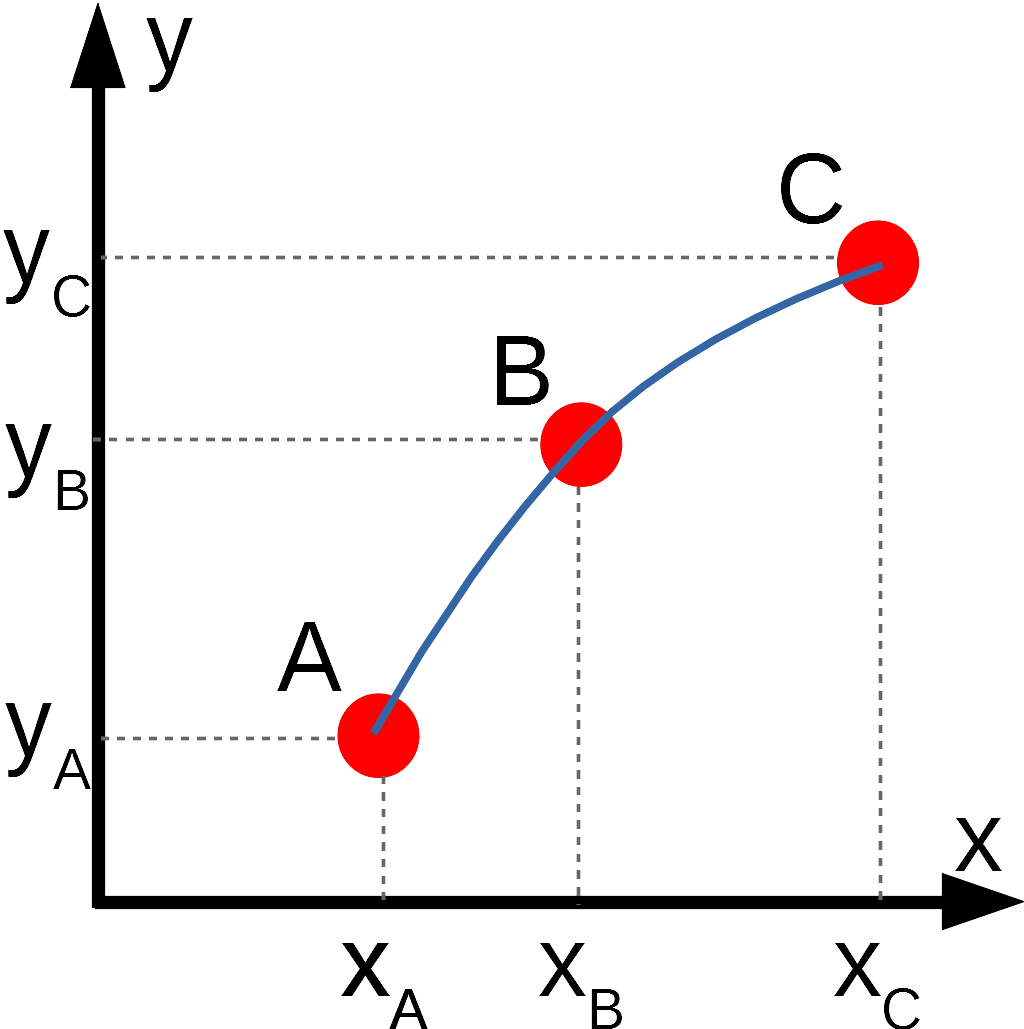
Un point se déplace dans un repère (O,$\overrightarrow{x}$,$\overrightarrow{y}$), les positions successives sont enregistrées tous les Δt secondes.

La vitesse d'un point dans un référentiel donné correspond à la variation de sa position par rapport au temps.

$\overrightarrow{V_B}=\frac{\overrightarrow{AC}}{2\times \Delta t}$

Dans le cas d'un mouvement plan, d'un intervalle de temps Δt constant entre chaque position, on peut écrire :

$\overrightarrow{V_B }=\overrightarrow{||V_B||}\times \overrightarrow{u}=\frac{\sqrt{{\left(x_C-x_A\right)}^2+{\left(y_C-y_A\right)}^2}}{2\times \Delta t}\times \overrightarrow{u}$

Le code python donné plus haut ne contient pas la façon de calculer la vitesse sur l'ensemble des points.
Si on regarde la fomule ci-dessus, on constate que pour calculer la vitesse au point B on utilise en fait les coordonnées de l'objet aux point A et C. Dans le programme sont définies 2 listes: x[ ] et y[ ].

Si on suppose que le point B est à la position i dans les listes x[ ] et y[ ], donc que ses coordonnées sont B(x[i],y[i]), alors le point A aura pour coordonnées A(x[i-1],y[i-1]) et le point C aura pour coordonnées C(x[i+1],y[i+1]).

Le vecteur vitesse s'écrit alors :

$\overrightarrow{V_B}\left(\frac{x_c-x_a}{2\Delta t},\frac{y_c-y_a}{2\Delta t}\right)=\left(\frac{x_{[i+1]}-x_{[i-1]}}{2\Delta t},\frac{y_{[i+1]}-y_{[i-1]}}{2\Delta t}\right)$

On peut donc compléter les 2 lignes permettant de calculer la vitesse pour tous les points :

🐍 Script Python

v_x.append((x[i + 1] - x[i - 1]) / (2 * delta_t))
v_y.append((y[i + 1] - y[i - 1]) / (2 * delta_t))

Cela signifie que l'on va progressivement ajouter aux listes v_x et v_y la valeur de la coordonnée x et y du vecteur vitesse $\overrightarrow{V_B}$.

Remarque

Puisque l'on utilise le point précédent et le point suivant, il y a 2 points dans un pointage dont on ne pourra pas déterminer la vitesse : la position initiale et la position finale, ce qui explique l'écriture de la boucle for i in range(1, len(x) - 1):

La formule pour calculer la vitesse en B est donc : $\overrightarrow{||V_B||}=\frac{\sqrt{{\left(x_{[i+1]}-x_{[i-1]}\right)}^2+{\left(y_{[i+1]}-y_{[i-1]}\right)}^2}}{2\times \Delta t}$.

En python, l'opérateur √ n'existe pas par défaut, en revanche en mathématiques \(\sqrt {x} = x^{0.5}\) ce qui se note en python x**0.5.

Avec $\overrightarrow{u}=\frac{\overrightarrow{AC}}{||\overrightarrow{AC}||}$ (cette façon d'écrire $\overrightarrow{u}$ permet de s'assurer qu'il a bien une longueur de 1).

Les flèches vertes représentent les vecteurs vitesse calculés par le script

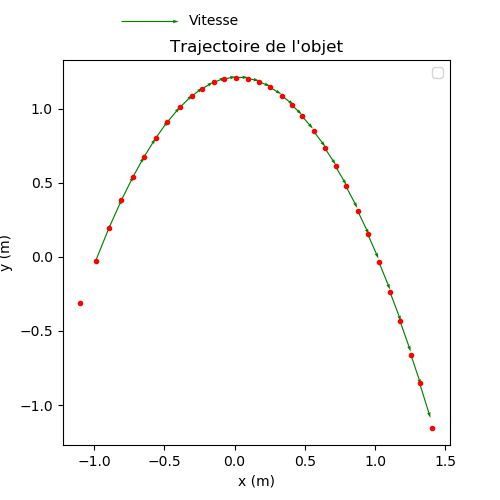
c. L'accélération

On constate que la vitesse varie sur ce tracé, on peut donc reprendre ce qu'on a écrit plus haut par rapport au tracé des vitesses pour maintenant représenter ces variations.

L'accélération a pour formule :

$\overrightarrow{A_B }=\overrightarrow{||A_B||}\times \overrightarrow{u}=\frac{\sqrt{{\left(v{x}_C-v{y}_A\right)}^2+{\left(v{x}_C-v{y}_A\right)}^2}}{2\times \Delta t}\times \overrightarrow{u}$

Le vecteur accélération s'écrit donc :

$\overrightarrow{A_B}=\left(\frac{v\_x_{[i+1]}-v\_x_{[i-1]}}{2\Delta t},\frac{v\_y_{[i+1]}-v\_y_{[i-1]}}{2\Delta t}\right)$

On peut donc compléter les 2 lignes permettant de calculer la vitesse pour tous les points :

🐍 Script Python

    a_x.append((v_x[i + 1] - v_x[i - 1]) / (2 * delta_t))
    a_y.append((v_y[i + 1] - v_y[i - 1]) / (2 * delta_t))

Cela signifie que l'on va progressivement ajouter aux listes a_x et a_y la valeur de la coordonnée x et y du vecteur accélération $\overrightarrow{A_B}$.

Remarque :

Puisque l'on utilise le point précédent et le point suivant, il y a maintenant 4 points dans un pointage dont on ne pourra pas déterminer l'accélération : les 2 premiers et les 2 derniers points, ce qui explique l'écriture de la boucle

for i in range(2 , len(v_x) - 2):.

Les flèches rouges représentent les vecteurs accélération calculés par le script

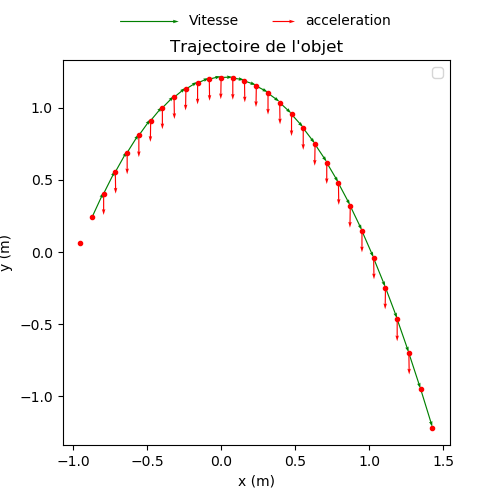
Afficher le code complet

🐍 Script Python

import matplotlib.pyplot as plt

# coordonnées de l'objet
# pas de temps (en secondes)
delta_t = 0.04  # a_indiquer
# Recopier ici les valeurs des positions des points obtenus dans l'atelier scientifique
x = []
y = []


# calcul du vecteur vitesse
if len(x) != len(y):
    print("problème de saisie, il n'y a pas le même nombre de points en x et en y !")

# Calcul du vecteur vitesse
v_x, v_y = [], []  # on crée 2 listes vides
for i in range(1, len(x) - 1):  # on va remplir les listes au fur et à mesure
    v_x.append((x[i + 1] - x[i - 1]) / (2 * delta_t))
    v_y.append((y[i + 1] - y[i - 1]) / (2 * delta_t))


# Calcul de la variation de vitesse
a_x, a_y = [], []  # on crée 2 listes vides
for i in range(1, len(v_x) - 1):  # on va remplir les listes au fur et à mesure
    a_x.append((v_x[i + 1] - v_x[i - 1]) / (2 * delta_t))
    a_y.append((v_y[i + 1] - v_y[i - 1]) / (2 * delta_t))


### Tracé des vecteurs normalisés
plt.rcParams["axes.formatter.use_locale"] = True
plt.figure(1, figsize=(5, 5))
vitesse = plt.quiver(x[1:-1], y[1:-1], v_x, v_y, color="green", width=0.003)
plt.quiverkey(vitesse, X=0.3, Y=1.1, U=10, label="Vitesse", labelpos="E")
acceleration = plt.quiver(x[1:-1], y[1:-1], a_x, a_y, color="red", width=0.003)
plt.quiverkey(acceleration, X=0.3, Y=1.1, U=10, label="acceleration", labelpos="E")
plt.plot(x, y, "r.")
plt.legend(loc="upper right")
plt.xlabel("x (m)")
plt.ylabel("y (m)")
plt.title("Trajectoire de l'objet")
plt.show()

Si le pointage a été parfaitement réalisé, vous devriez obtenir l'image ci-dessus...
... mais en réalité, vous obtiendrez quelque chose comme cela :

Les flèches rouges représentent les vecteurs accélération calculés par le script

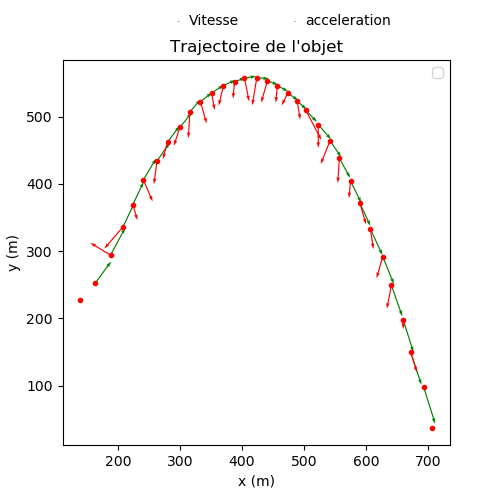
Que se passe-t-il ?

Le fait de calculer les variations de position puis le variations de vitesse démultiplie les petites erreurs que l'on fait lors du pointage, cela est inévitable.
Pour obtenir le premier graphique, il m'a donc fallu tricher, en modélisant la trajectoire issue du pointage. Les vecteurs sont ensuites tracés en utilisant les points issus de cette modélisation (ce sont ceux disponibles dans le script corrigé)