Mouvement et interactions

0 - Utilisation de pymecavideo

Pymecavideo est le logiciel que nous utiliserons en mécanique pour étudier les mouvements.
Il est relativement simple d'utilisation, voici un rapide tutoriel pour l'utiliser :

I- Mouvement et référentiel

1) Introduction

Incident survenu dans le TGV Paris-Lyon

Schéma

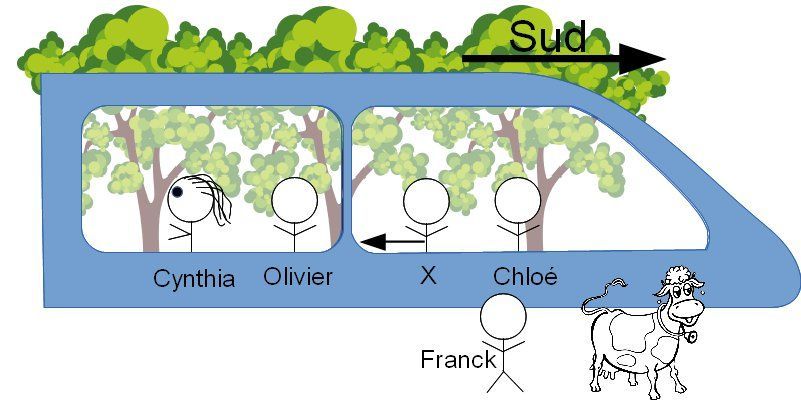
L'inspecteur Watson enquête sur tous les incidents, même les plus minimes. Voici un extrait du rapport d'une de ses enquêtes.

Les faits : Nous sommes le 1er avril 2021. Alors que Chloé dormait tranquillement, un individu, que l’on prénommera X, lui a collé un poisson d’avril sur le front.

Les témoignages recueillis :

• Alice - "La victime était immobile"
• Olivier - "X s’éloignait vers le nord"
• Franck - "La victime et X se déplaçaient très rapidement vers le sud"
• La vache - "Meuh"
• Cynthia -"Je n'ai rien vu car j'étais en train de regarder les arbres qui reculaient"

Quel imbroglio ! Et pourtant aucun témoin n'a menti (sauf peut-être la vache) ou n'est fou.
Aidez l’inspecteur Watson à reconstituer la scène de l’incident.

On voit qu'une même scène peut être décrite de façon très différente en fonction du lieu où l'on se trouve. Il est donc nécessaire avant toute étude de mouvement de préciser par rapport à quel référence on l'étudie.

2) Le référentiel

C'est ce par rapport à quoi l'on va étudier un mouvement. Il n'y a pas de référentiel absolu, mais on peut en citer 3 qui sont souvent utilisés :

• Le référentiel terrestre rattaché au sol (salle de classe, laboratoire)
  Il est utilisé pour les mouvements terrestres (vélo, voiture) et aériens (avion, oiseau)

• Le référentiel géocentrique, positionné au centre de la Terre, mais ne tournant pas avec elle. Ainsi, le référentiel terrestre tourne autour du référentiel géocentrique en 24h.
  Il est utilisé pour le mouvement des satellites ou de la Lune.

• Le référentiel héliocentrique, positionné au centre du Soleil, mais ne tournant pas avec lui.Le référentiel géocentrique tourne autour de lui en 365j.
  Il est utilisé dans l'étude du mouvement des planètes, comètes, astéroïdes...

Calculer la vitesse à laquelle se déplace un élève assis dans une salle de cour dans :

1. le référentiel terrestre
2. le référentiel géocentrique
3. le référentiel héliocentrique

Corrigé

1. Dans ce référentiel, l'élève est immobile : $v=0 \mathrm{km}·h^{-1}$
2. L'élève fait le tour du référentiel en 24h.
   Il parcourt pendant ce temps le périmètre terrestre, soit à peu près 40 000 km.
   Sa vitesse est donc : $v=\frac{d}{t}=\frac{\mathrm{40000km}}{\mathrm{24h}}=\frac{\mathrm{40000km}}{\mathrm{24h}}=\mathrm{1700km/h}$
3. L'élève fait le tour du référentiel en 365j, soit $365\times 24=8760h$
   Pendant ce temps il parcourt l'orbite de la Terre autour du Soleil. La distance Terre-Soleil = 150 000 000 km.
   L'orbite a donc un périmètre de $P=2\times \pi \times R=2\times \pi \times \mathrm{1,5}\times {10}^8\mathrm{km}=\mathrm{9,4}\times {10}^8\mathrm{km}$
   Sa vitesse est donc : $v=\frac{d}{t}=\frac{\mathrm{9,4}\times {10}^8\mathrm{km}}{\mathrm{8760h}}=\mathrm{107000km/h}$

3) Le repère

Pour décrire correctement le mouvement d'un objet dans un référentiel choisi, il faut y choisir un repère orthonormé.
Ce repère n'est en revanche pas forcément orienté selon la verticale et l'horizontale. Il peut être plus judicieux de l'orienter en fonction du mouvement étudié pour simplifier les calculs.

Etude de la chute d'une balle	Etude d'une balle qui roule sur un plan incliné

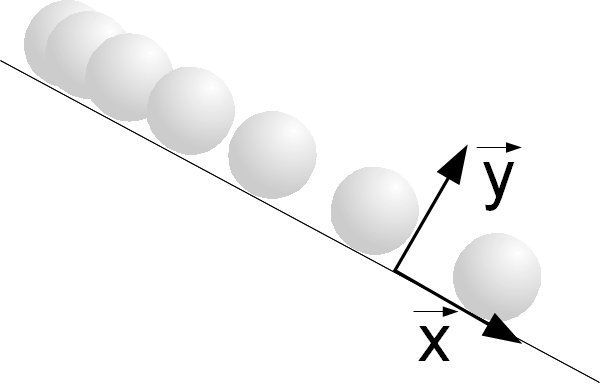4) La trajectoire

Il est n'est toujours possible de parler de la trajectoire d'un objet entier, on parle donc de la trajectoire d'un point précis appartenant à l'objet.

Trajectoire de deux points d'un frisbee lancé

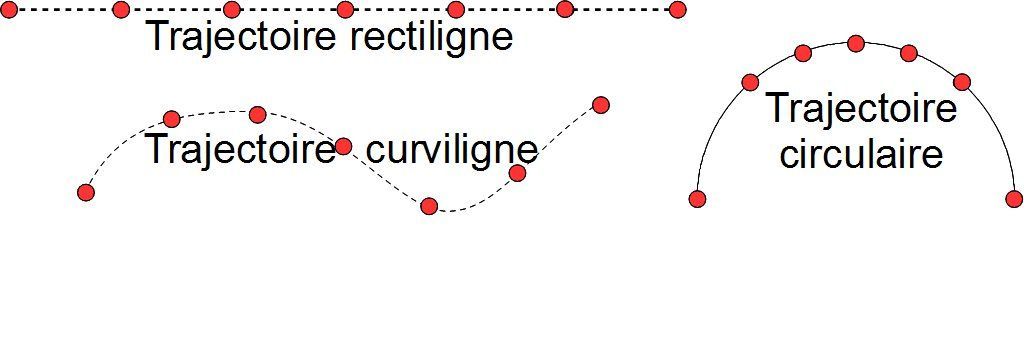
On distingue trois types de trajectoires :

• Trajectoire rectiligne lorsque les points sont alignés
• Trajectoire circulaire lorsqu'ils sont placés sur un même cercle
• Trajectoire curviligne dans les autres cas

5) La vitesse

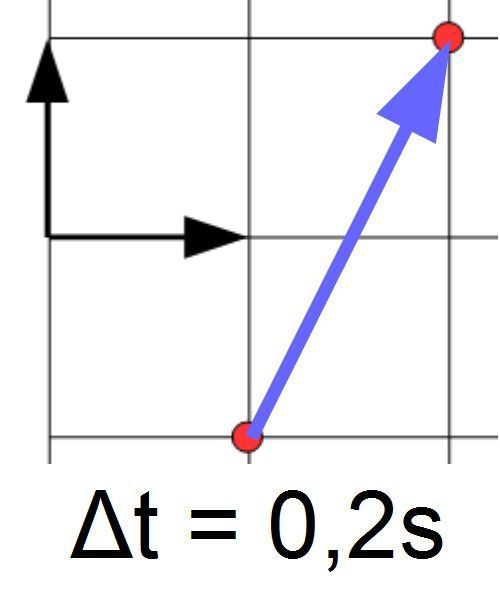
La vitesse d'un point correspond à la distance que ce point a parcouru dans un intervalle de temps donné :

$\mathrm{vitesse}=\frac{\mathrm{distance}}{\mathrm{temps}}$

Dans un exemple comme le cas ci-contre, il faut utiliser la relation de Pythagore pour calculer la vitesse :

$\mathrm{vitesse}=\frac{\sqrt{{\mathrm{(distance\; sur\; x)}}^2+{\mathrm{(distance\; sur\; y)}}^2}}{\mathrm{temps}}$

II - Etude informatique du mouvement

1) Logiciels de chronophotographie

La chronophotographie consiste à prendre des images à intervalles réguliers afin de pouvoir étudier un mouvement. Cette méthode a été inventée en 1878 (si vous voulez en savoir plus : vous pouvez aller faire un tour sur Wikipédia).

Il existe maintenant des applications permettant de le faire simplement à l'aide de votre téléphone comme Motion Shot©
( sur Android ou sur iOS).

Sur ordinateur, on utilise en classe l'Atelier Scientifique de Jeulin©. Celui-ci étant payant (et obsolète), il vous est possible d'utilise le programme Pymecavideo, que vous pouvez télécharger en cliquant sur l'icône ci dessous :

Pymecavideo 7.2.1.1

2) Etude du mouvement à l'aide de pymecavideo

Etudions cette video :

un velo roulant à vitesse constante

Un point blanc est dessiné sur le pneu. Dans le référentiel lié au vélo, ce point trace une trajectoire circulaire uniforme, mais dans le référentiel terrestre ?

3) Vitesse et langage de programmation

Le calcul présenté précedemment est rapidement fastidieux si on le fait à la main. Un langage de programmation va permettre de faire réaliser ces opérations par l'ordinateur.
Dans le TP n°13, on a pointé la trajectoire d'une balle lancée "en cloche", on peut récupérer les coordonnées des positions successives et les intégrer dans le programme :

🐍 Script Python

# pas de temps de la vidéo
delta_t=0.04
# coordonnées de l'objet
x=[-0.954, -0.874, -0.795, -0.716, -0.636, -0.557, -0.477, -0.398, -0.319, -0.239, -0.16, -0.081, -0.001, 0.078, 0.157, 0.237, 0.316, 0.395, 0.475, 0.554, 0.634, 0.713, 0.792, 0.872, 0.951, 1.03, 1.11, 1.189, 1.268, 1.348, 1.427]
y=[0.06, 0.24, 0.405, 0.555, 0.689, 0.808, 0.911, 0.999, 1.072, 1.129, 1.171, 1.198, 1.209, 1.205, 1.185, 1.15, 1.1, 1.035, 0.954, 0.858, 0.746, 0.619, 0.477, 0.319, 0.146, -0.043, -0.246, -0.465, -0.7, -0.95, -1.215]

Il est possible de tracer ces valeurs sur un graphique à l'aide de la bibliothèque matplotib :

🐍 Script Python

from matplotlib import pyplot as plt
plt.rcParams['axes.formatter.use_locale'] = True
plt.figure(1, figsize=(5, 5))
plt.plot(x,y,"r.")
plt.legend(loc='upper right')
plt.xlabel("x (m)")
plt.ylabel("y (m)")
plt.title("Trajectoire de l'objet")
plt.show()

Une foix executé, ce programme affichera ce graphique :

Les points rouges représentent les positions successives de la balle

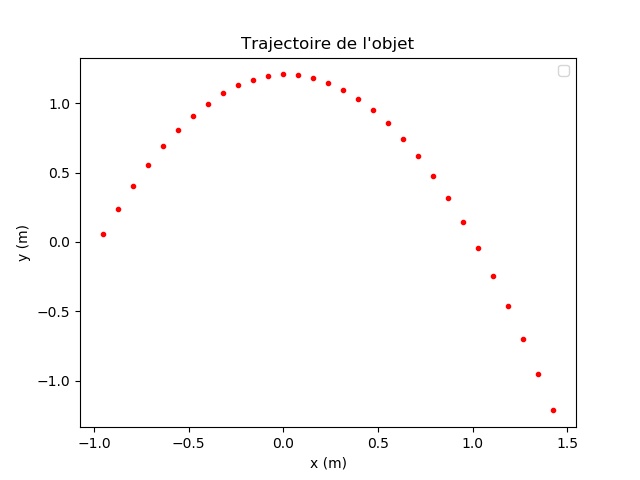
Maintenant que l'on a la position de l'objet on peut demander au programme de calculer la vitesse de la balle entre chaque point :

Représentation de la vitesse par des vecteurs

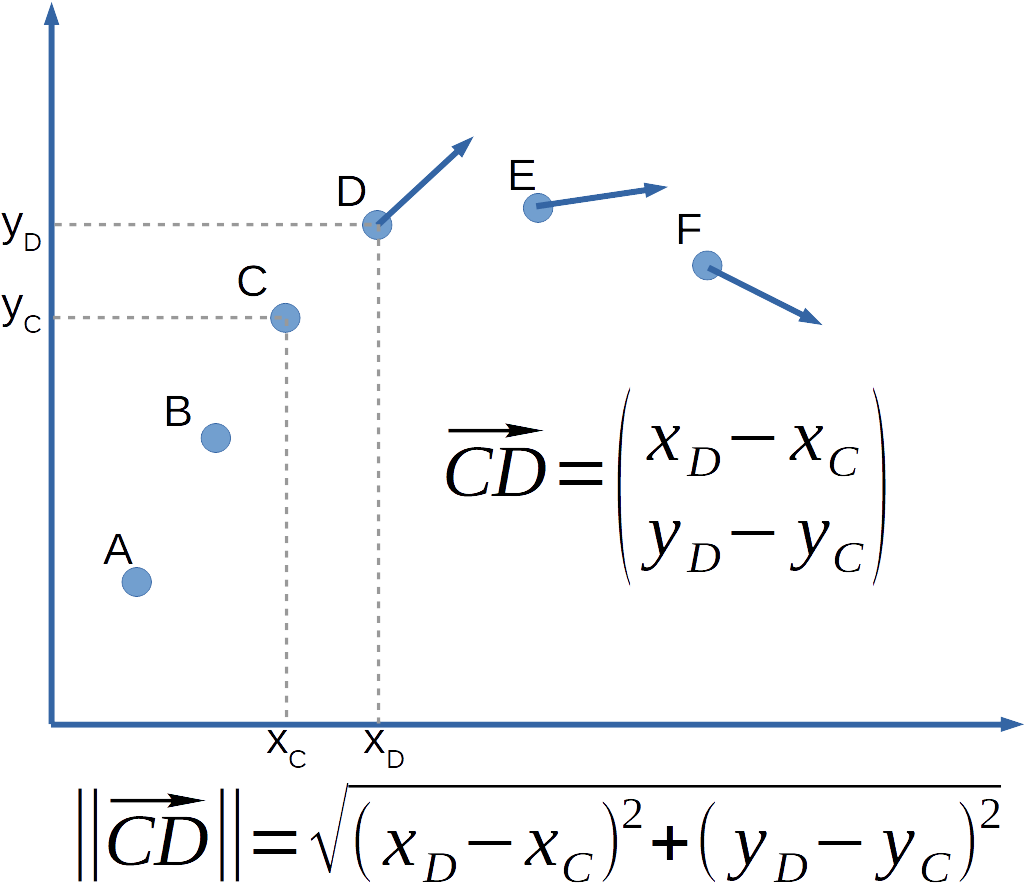
Dans le schéma ci-dessus, on montre comment calculer les coordonnées du vecteur déplacement entre 2 points.
La vitesse en un point donné correspond au rapport entre le vecteur formé par ce point et le point précédent et l'écart de temps séparant les 2 positions.
Cela s'écrit :

vitesse	notation vectorielle
\(v_C = \frac{\sqrt{(x_D - x_C)^2 + (y_D - y_C)^2}}{\Delta t}\)	\(\vec{v_C} = \begin{pmatrix}\frac{x_D - x_C}{\Delta t} \\ \frac{y_D - y_C}{\Delta t}\end{pmatrix}\)

III- Les forces

1) Introduction

Représenter les forces

• Télécharger l'activité : Cliquer ici

2) Présentation

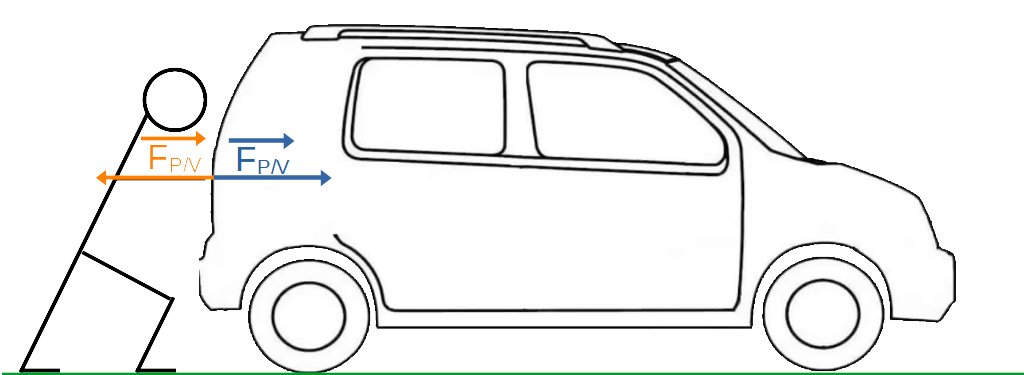
Pierre pousse sa voiture qui ne veut pas démarrer. En se mettant derrière, il exerce une action mécanique, que l'on représente ainsi :

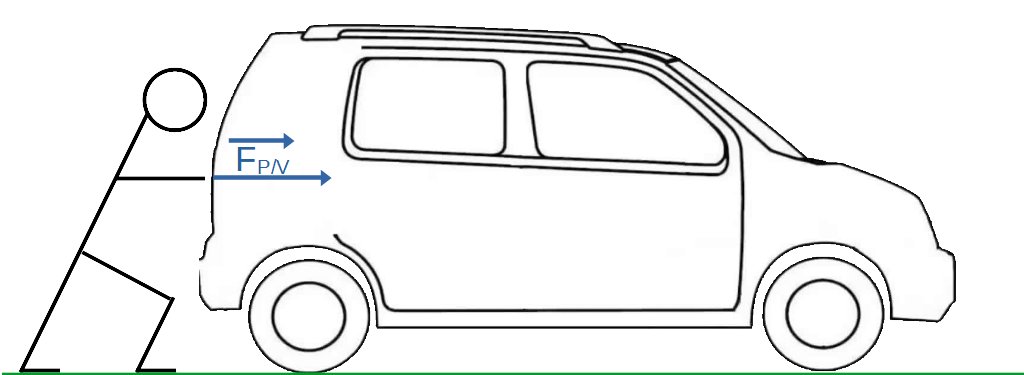
Représenter une force

Une action mécanique exercé par un objet A sur un objet B est représenté par une flèche dont :

• (hors programme) l'origine est le point d'application de la force,
• La direction et le sens sont celles de la force
• La longueur est proportionnelle à l'intensité de la force.

Notation et unité

L'action mécanique exercé par un objet A sur un objet B se note ${\displaystyle \stackrel{\to <!--\; \to \; -->}{F_{A/B}}}$.

L'unité du Système International pour exprimer une force est le newton (N).

2) Principe d'action-réaction

Ce que l'on appelle aussi la 3^eme loi de Newton et que l'on peut trouver contre-intuitive s'énonce ainsi :

3° loi de Newton

Si un objet A exerce sur un objet B une action mécanique ${\displaystyle \stackrel{\to <!--\; \to \; -->}{F_{A/B}}}$, alors cette objet B exercera toujours en retour une action mécanique ${\displaystyle \stackrel{\to <!--\; \to \; -->}{F_{B/A}}}$ égale et opposée à ${\displaystyle \stackrel{\to <!--\; \to \; -->}{F_{A/B}}}$.

C'est contre-intuitif, mais on a toujours

$\stackrel{\to <!--\; \to \; -->}{F_{A/B}}=-<!--\; -\; -->\stackrel{\to <!--\; \to \; -->}{F_{B/A}}$

Dans le cas précédent, cela signifie que quelle que soit la situation (la voiture a le frein verrouillé, la voiture avance ou la voiture recule), on aura toujours le schéma suivant :

3) Principe d'inertie

1° loi de Newton

Si un objet n'est soumis à aucune force ou bien si elles se compensent, alors sa trajectoire est rectiligne uniforme (ou immobile)

Comprendre le principe d'inertie

L'animation simulameca est disponible sur le site de Tristan Rondepierre : Cliquer ici pour y accéder

Corollaire

Si un objet n'a pas une trajectoire rectiligne uniforme (l'immobilité est un cas particulier) alors on peut en déduire qu'une ou plusieurs forces s'exercent sur elle.

Deviner l'invisible

Cela n'en a pas l'air, mais cette proposition est très puissante : elle permet à elle seule de conclure à l'existence d'une force invisible s'exerçant sur la Lune et expliquant sa rotation autour de la Terre. Cette force est bien évidemment l'interaction gravitationnelle.

C'est par cette méthode que l'on a découvert le trou noir central de notre galaxie appelé Sgr A*

4) Application à Pierre et sa voiture

Si l'on revient à l'exemple précédent, on pourrait se demander comment il est possible d'expliquer le mouvement à partir des forces, puisque quel que soit l'effet (la voiture avance, recule ou est immobile) on a toujours $\overrightarrow{F_{A/B}}=-\overrightarrow{F_{B/A}}$.

En réalité, si ces forces se compensent et que la voiture se met en mouvement, on doit en conclure que ce qui explique le mouvement n'est pas représenté !
On est donc poussé à rechercher ces forces :

• L'action du poids P→
• La réaction du sol ${\displaystyle \overrightarrow{F_{S/V}}}$
• et surtout : les frottements du sol ${\displaystyle \overrightarrow{{\mathrm{F\text{'}}}_{S/V}}}$

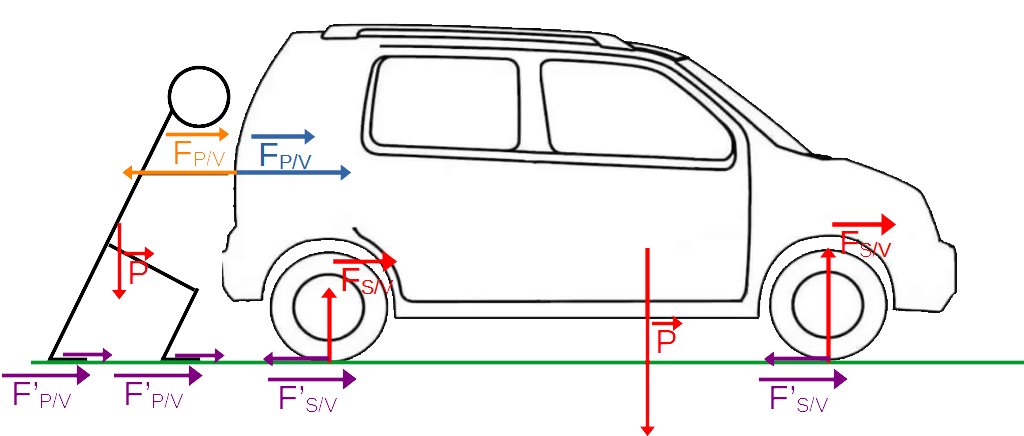
Une fois le schéma complété on peut conclure : en réalité ce qui va mettre ou non la voiture en mouvement c'est l'écart entre les forces de frottement entre les pneus et le sol d'une part et entre les chaussures de Pierre et le sol d'autre part.

5) Lister les forces s'exerçant sur un objet

DOI

Schéma

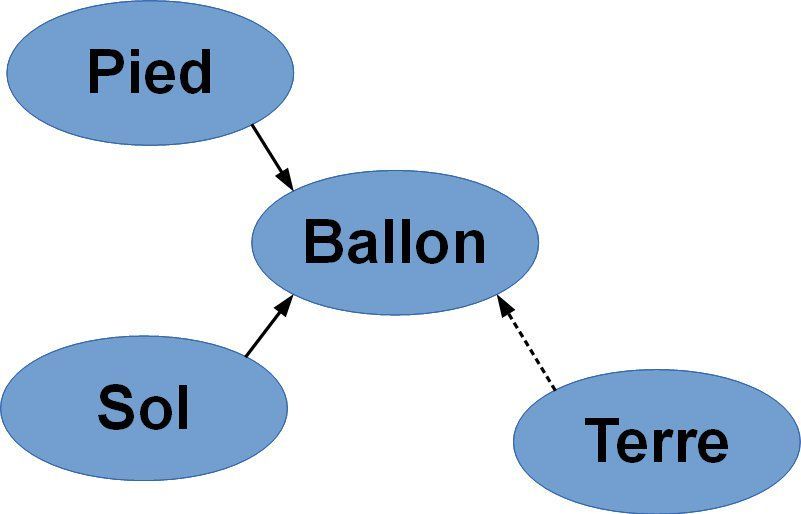
Pour ne pas oublier une force lorsque l'on énumère celles qui s'exercent sur un objet, on peut utiliser un diagramme objet-interaction (ou DOI).

Par convention une force de contact est tracée en trait plein et une force à distance en pointillés.

On peut représenter l'ensemble des forces s'exerçant sur le ballon dans le schéma ci-contre :

6) Relation entre la masse et le poids

Définition

Le poids d'un objet est la force d'attraction qu'exerce la masse de la Terre sur cet objet.

Puisque le poids est une force, il ne s'exprime pas en grammes ou en kilogrammes (ça, c'est la masse) mais en newtons (N).

• La masse est une grandeur qui est propre à l'objet. Elle ne dépend que de l'objet et pas du lieu où il se trouve.
• Le poids est une grandeur qui dépend de la masse de l'objet, mais également du lieu où il se trouve.

On ne pèse pas le même poids que l'on soit sur Terre ou sur Mars, ou même que l'on se trouve à Sète ou à Kourou (Guyanne). En revanche, notre masse restera la même où que l'on se trouve.

Tp virtuel masse-poids

Pour étudier la relation entre la masse et le poids, vous pouvez faire ce "TP virtuel" réalisé par Stéphane Bonnaud (le site sciencesgrandsud mentionné ne semble plus exister)

Les fichiers forces.swf (cliquer pour télécharger) (auteur : Adrien WILLM) et TPvirtuel_poids_masse.swf (cliquer pour télécharger) sont des fichiers au format Acrobat flash. Comme ce forma a été abandonné par Adobe, il est nécessaire si vous n'arrivez pas à l'ouvrir de récupérer ce logiciel : Adobe Flash Player 10

7) Des forces particulières

La gravité

Son point d'application est le centre de gravité de l'objet, sa direction est la verticale du lieu et son sens vers le centre de la Terre.
Son intensité, qu'on appelle le poids vaut :
P(N) = masse (kg) × Intensité de pesanteur = m × g
avec g=9.8N.kg^-1 sur Terre.

La force électromagnétique

Il est difficile d'étudier cette force en seconde car sa direction, son sens, sont intensité et son point d'application sont variables.

La poussée d'Archimède

Contrairement aux deux précédentes forces, la poussée d'Archimède est une force de contact. Elle est exercée en tout point de la surface de l'objet qui est immergé dans le fluide qui l'exerce. Plutôt que de représenter une infinité de points à la surface de l'objet, on ne représente qu'une seule force, au centre géométrique de la partie immergée de l'objet.
La poussée d'Archimède s'oppose à l'attraction, sa direction est donc verticale et son orientation vers le haut. Son intensité est égale au poids du volume d'eau déplacé par l'objet.

Application

Jean-Pierre a une masse de 90 kg et un volume corporel de 92L.

1. Calculer son poids

Jean-Pierre plonge dans sa piscine et s'immerge complètement, immobile.

1. Calculer la poussée d'Archimède qu'exerce l'eau sur Jean-Pierre.
2. Conclure

Données :
g = 9.8N.kg^-1; ρ_eau=1000kg.m^-3

Corrigé

1. Le poids de Jean-Pierre vaut : $\mathrm{P(N)}=\mathrm{masse\; (kg)}\times \mathrm{Intensité\; de\; pesanteur}=m\times g=90\times \mathrm{9,8}=882N$

 

1. Jean-Pierre a un volume corporel de 92L, il déplace donc ce même volume d'eau.
   La masse d'eau vaut donc $\mathrm{m(kg)}=\rho \times V=1000{\mathrm{kg.m}}^{-3}\times 0.092m^3=92\mathrm{kg}$
   Le poids de ce volume d'eau vaut $\mathrm{P(N)}=\mathrm{masse\; (kg)}\times \mathrm{Intensité\; de\; pesanteur}=m\times g=92\times \mathrm{9,8}=\mathrm{901,6}N$
   
2. Jean-Pierre n'est soumis qu'à son propre poids (882N) et la poussée d'Archimède (901.6N). Il va donc remonter à la surface puisque la poussée d'Archimède est plus forte que son poids.